LOS NÚMEROS ENTEROS
LOS NÚMEROS ENTEROS (I)
Los
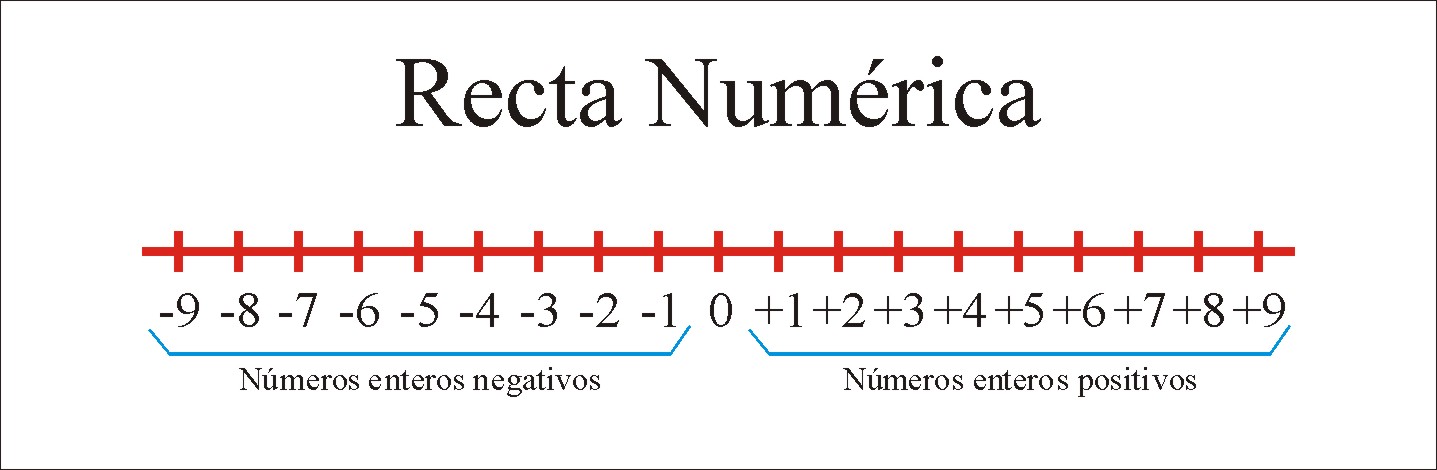
números positivos se representan en una recta horizontal a la
derecha del punto 0, y los negativos a la izquierda.
Dos
números que sólo se diferencian en su signo, se llaman opuestos.
Todos los números tienen su opuesto.
Por
ejemplo:
El
opuesto de +3 es –3 . El opuesto de –12 es +12.
NÚMEROS ENTEROS
COORDENADAS DE UN PUNTO
Los números enteros son el conjunto de números formado por los números positivos (+1, +2, +3...), los negativos (-1, -2, -3...) y el cero.
COMPARACIÓN DE NÚMEROS ENTEROS
Para comparar los números enteros nos fijaremos en la recta numérica.
Cualquier número entero es mayor que otro situado a su izquierda.
-1 > -7 -5 < +6 +3 > +2
- De
dos números positivos es mayor el más alejado del punto 0
+6
> +2
-
De dos números negativos es mayor el más próximo al punto 0
-3
> -7
-
Cualquier punto positivo es mayor que otro negativo.
+1
> -3
-
El 0 es menor que cualquier número positivo y mayor que los negativos.
+3
> 0 0 > -3
VALOR
ABSOLUTO
El
valor absoluto de un número entero es el que posee prescindiendo del
signo.
Ejemplos:
(+12)=
12 (-8)= 8
SUMA DE NÚMEROS ENTEROS
Para sumar
dos números enteros con el mismo signo se
suman sus valores absolutos y se le pone el mismo signo.
(-6) + (-8) =
-14 (+3) + (+9) = +12
Para sumar
dos números enteros con distinto signo se
restan sus valores absolutos y se le coloca el signo del de mayor
valor absoluto.
(-3) + (+4) = +1 (-6) +
(+2) = - 4
(+7) + (-9) = -2 (+7) +
(-2) = +5
RESTA
DE NÚMEROS ENTEROS
Restar dos números
enteros equivale a sumar al minuendo el opuesto del sustraendo.
Ejemplos:
(+
4) – (+7) = +4 – 7 = -3
(-
7 ) – ( - 2) = -7 + 2 = -5
Si
el paréntesis va precedido del signo +
los números del
interior del paréntesis conservarán su signo:
+
7 +(- 4 + 6 – 7) = +7 – 4 + 6 – 7 = +2
Si
el paréntesis va precedido del signo –
los números del
interior del paréntesis cambiarán de signo:
+
7 - (- 4 + 6 – 7) = +7 + 4 - 6 + 7 = +12
COORDENADAS DE UN PUNTO
Para
expresar las coordenadas de un punto, aparecen entre paréntesis;
primero se marca la coordenada del eje horizontal (x), y luego la
correspondiente al eje vertical (y).
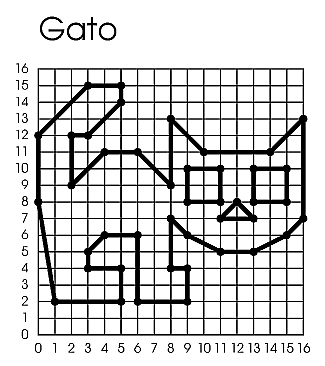
Actividad
Para comprobar si sabemos utilizar las coordenadas intenta dibujar este gato marcando cada uno de sus coordenadas con un punto. Después llamaremos a cada punto con una letra del abecedario. Por último, escribe los puntos de cada coordenada.
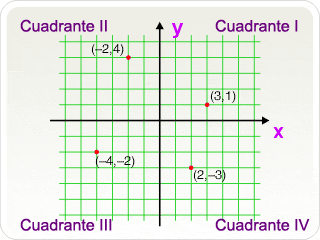
COORDENADAS CARTESIANAS
Son dos rectas
perpendiculares que dividen el plano en cuatro cuadrantes, y que se
cortan entre sí en el llamado punto de origen cartesiano (o).
Sus dos ejes se pueden
denominar también como eje x o de abcisas (horizontal), y eje y o de
ordenadas (vertical).
Para representar un punto en el plano se ponen dos números entre paréntesis, por ejemplo (3,1). El primer número se corresponde con el eje x, y el segundo número con el eje y.
(TRUCO: hay que recorrer el pasillo antes de subir las escaleras)
Para representar un punto en el plano se ponen dos números entre paréntesis, por ejemplo (3,1). El primer número se corresponde con el eje x, y el segundo número con el eje y.
(TRUCO: hay que recorrer el pasillo antes de subir las escaleras)
PLANO CARTESIANO
TRAZADO DE PUNTOS EN UN CUADRANTE
COORDENADAS DE UN PUNTO EN EL PLANO




No hay comentarios:
Publicar un comentario