Al
hacer una división de números enteros pueden ocurrir dos cosas.
- Será una división exacta si su resto es 0. 10: 5 = 2
- Será una división entera si su resto es diferente de 0.
- Ejemplo: 10:3= 3 r =1
MÚLTIPLOS DE UN NÚMERO
Los
múltiplos
de un número
se obtienen multiplicando dicho número por los números naturales:
0, 1, 2, 3, 4, 5, 6...
Un
número a
es múltiplo de otro b
si la división a:
b
es exacta.
Por
ejemplo:
Si
queremos comprobar si el número 48 es múltiplo de 4, lo dividimos:
48
: 4=12 Como es una división exacta, podemos decir que el 48 es
múltiplo de 4.
Los
múltiplos de un número son infinitos.
Múltiplos
de 2={0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 ..........}
Múltiplos
de 3={0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36 ........}
ACTIVIDADES
ACTIVIDAD MÚLTIPLOS I
ACTIVIDAD MÚLTIPLOS II
ACTIVIDAD MÚLTIPLOS III
DIVISORES DE UN NÚMERO
Divisor
de un
número es aquel que está contenido en él, un número exacto de
veces. Al dividir un número por sus divisores el resto es cero.
El
5 es divisor de 15 porque lo contiene tres veces. 15 : 5 = 3 y resto
0.
Observa
la relación: 5 es divisor
de
15 y 15 es múltiplo
de
5
Un
número es divisible
por
otro cuando lo contiene un número exacto de veces.
Un
número b es divisor de otro a si la división a:b es exacta.
Si
b es divisor de a, a es múltiplo de b, y si a es múltiplo de b, b
es divisor de a.
A=20
B=
5
20:5=
4 5 es divisor de 20.
20
es múltiplo de 5 porque 5 X4 = 20.
RECUERDA
PÁGINA 51:CRITERIOS DE DIVISIBILIDAD
Nos
permiten saber de un modo sencillo cuando un número es divisible por
otro.
| NÚMERO |
CRITERIO
|
2
|
Un número es divisible por 2 cuando acaba en 0 o en cifra par. |
3
|
Un número es divisible por 3 cuando la suma de sus cifras da 3, o múltiplo de 3. |
5
|
Un número es divisible por 5 cuando acaba en 0 ó 5. |
6
|
Un número es divisible por 6 si es divisible por 2 y 3. |
10
|
Un número es divisible por 10 cuando acaba en 0. |
MÁXIMO COMÚN DIVISOR
Máximo
común divisor (M.C.D.) de
dos o más números es el mayor de los divisores
comunes
de dichos números.
Ejemplos:
M.C.D.
(12, 15) = 3
D12=
1,2,3,4,6,12.
D15=
1,3,5,15.
NÚMEROS PRIMOS Y COMPUESTOS
Un número es primo si solo tiene dos divisores, el 1 y él mismo.
CALCULAR EL MCD Y EL mcm CON FACTORES PRIMOS
Para calcular el MCD de dos o más números, los descomponemos en factores primos, y después cogemos los factores comunes elevados al menor exponente.
Ejemplos:
MCD
mcm




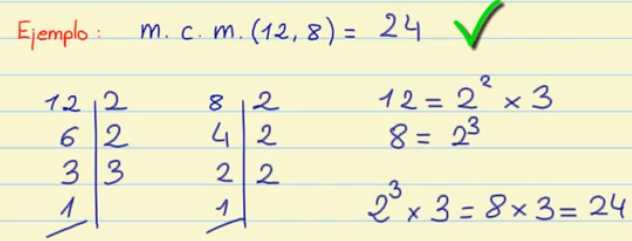
No hay comentarios:
Publicar un comentario